内容

    1. ノート一覧
    2. 数学
    3. 微分積分

    面積分・体積分

    Dr. SSS 2020/06/21 - 15:20:40 14352 微分積分
    はじめに

    ここでは，図形の面積や体積を求める積分方法と，関数の面積分・体積分について解説する。


    keywords: 面積分, 体積分, 微分積分, ベクトル解析

    面積計算

    面積要素

    任意の曲線の長さ$l$は，$N$個の微小な線分$\Delta l_i, \ (i=1,2,...,N)$に分割して

    \begin{align} \sum_{i=1}^N \Delta l_i \end{align}

    と，和を取り，分割数を無限にする極限$N\to \infty$を取ることで

    \begin{align} l=\lim_{N\to \infty} \sum_{i=1}^N \Delta l_i =\int dl \end{align}

    と求められるのであった（『線積分』参照）。 同様の考え方により，平面上の任意の面積$S$が，微小な面積$\Delta S_i$を用いて

    \begin{align} \sum_{i=1}^N \Delta S_i \end{align}

    とし，分割数を無限にする極限により

    \begin{align} \label {eq:S} S=\lim_{N\to \infty} \sum_{i=1}^N \Delta S_i =\int_S dS \end{align}

    と求められる。 この$dS$を面積要素（surface element）という。

    容易な例として，直線直交座標系を取り，原点から$x$軸方向に長さ$a$，$y$軸方向に長さ$b$を持つ長方形の面積の計算を考えてみる。 このとき，面積要素は$dx dy$と表せるから総面積は

    \begin{align} \int_0^b dy \int_0^a dx = a\int_0^b dy =ab \end{align}

    と計算できる。


    極座標と円や球の表面積

    今度は円の面積を考えてみよう。 この例では，直線直交座標系を取るのではなく，極座標（polar coordinates）と呼ばれる別の座標を選択したほうが計算が楽になる。 位置$(x,y)$は，原点からの距離$r$と偏角$\theta$を用いて

    \begin{align} x=& r\cos{\theta} \\ y=& r\sin{\theta} \end{align}

    で表せるから，$(r,\theta)$によって位置を指定することもできる（三角関数の復習はコチラから）。 この変数の組を平面極座標という。 直線直交座標系とは異なり，この座標系での面積要素は，単に独立変数の微小量の積$drd\theta$とはならない（そもそも$\theta$は無次元なので$drd\theta$は面積の次元になっていない）。

    正しい面積要素は以下のように求められる。 半径$r$の円は，$r$方向，$\theta$方向に分割すると，図1の点$A$，$B$，$C$，$D$で囲まれたような図形の集まりに分けられる。 孤$CD$の長さは$(r+\Delta r)\Delta \theta$であり，これに$\Delta r$をかけたものは$\Delta r (r+\Delta r)\Delta \theta$となる。 そのため，$\Delta r$，$\Delta \theta$を微小に取った場合，孤$AB$の長さ$r\Delta \theta$に幅$\Delta r$をかけたものとの差は$\Delta $の3次の量となり，無視できる。 すなわち，面$ABCD$の面積は底辺$\Delta r$，高さ$r\Delta \theta$の長方形の面積で近似できる。 この面積は，図中に青色で示した長方形の面積に対応する。

    図1：平面極座標における面積要素のイメージ

    よって，$\Delta r$，$\Delta \theta$をそれぞれ無限小にとってやれば，平面極座標系での面積要素が

    \begin{align} \label {dS_polar} dS=rdrd\theta \end{align}

    と得られる。 一般的な説明は別でするが，ここで(\ref{dS_polar})に$drd\theta$との差異として含まれる$r$は，座標変換一般の文脈でJacobianと呼ばれる量に対応する。 (\ref{dS_polar})を用いると，円の面積が直ちに

    \begin{align} \int_0^r rdr \int_0^{2\pi} d\theta = \frac{r^2}{2}\times 2\pi=\pi r^2 \end{align}

    と得られる。

    この手法は平面だけでなく，3次元中の曲面の計算にも用いることができる。 例として，球の表面積を求めてみよう。 この場合も，座標は極座標を用いるのが都合がいい。 3次元では，位置$(x,y,z)$はもう1つ角度変数$\phi$を追加して

    \begin{align} x=&r\sin{\theta}\cos{\phi} \\ y=&r\sin{\theta}\sin{\phi} \\ z=&r\cos{\theta} \end{align}

    で指定できる（図2左）。 このとき，球の面積要素は

    \begin{align} \label {eq:3dS} dS=r^2 \sin{\theta} d\theta d\phi \end{align}

    で与えられる（図2右）。

    図2：直線直交座標$(x,y,z)$と3次元極座標との対応（左）および3次元極座標における面積要素のイメージ

    これを，$\theta$方向に$0$から$\pi$，$\phi$方向に$0$から$2\pi$まで積分する。

    \begin{align} S=r^2 \int_0^\pi \sin{\theta} d\theta \int_0^{2\pi} d\phi \end{align}

    $\phi$についての積分からはそのまま$2\pi$が得られ，$\theta$についての積分は

    \begin{align} \int_0^\pi \sin{\theta} d\theta =\left. -\cos{\theta} \right|^\pi_0 =2 \end{align}

    となるから，半径$r$の球の表面積が

    \begin{align} \label {eq:sphere_area} S=4\pi r^2 \end{align}

    と得られる。


    体積計算

    前節の議論は，3次元空間中の体積計算にも拡張できる。 (\ref{eq:S})に対応するのは，求める体積を$V$とすると

    \begin{align} V=\lim_{N\to \infty} \sum_{i=1}^N \Delta V_i =\int_V dV \end{align}

    となる。面積分における面積要素に対応する微小体積$dV$は体積要素（volume element）と呼ばれる。

    例として今度は球の体積を求めてみる。 体積要素は球の面積要素(\ref{eq:3dS})に厚み$dr$を持たせて

    \begin{align} r^2 dr \sin{\theta} d\theta d\phi \end{align}

    とできる。 これを積分したものは，(\ref{eq:sphere_area})を$r$方向に積分したものに等しく，半径$r$の球の体積が

    \begin{align} V=4\pi \int r^2 dr=\frac{4}{3}\pi r^3 \end{align}

    と求まる。


    面積分・体積分

    ここまでの考えを利用すると，ある関数$f$の面$S$および積分$V$に渡る積分をそれぞれ

    \begin{align} \int_S f dS \end{align}

    および

    \begin{align} \int_V f dV \end{align}

    で計算することができる。 これらをそれぞれ，関数$f$の面積分（surface integral）および体積分（volume integral）という。

    また，面から流出（または流入）するエネルギーや物質の量を計算したい時など，方向を含めた積分値が知りたい時もある。 その場合，計算したいベクトル量を$\bm{A}$，面と垂直で外向きの単位ベクトルを$\bm{n}$とすると，求める量は

    \begin{align} \int_S \bm{A}\cdot \bm{n} dS \end{align}

    で計算できる。 あるいはこの方向の情報を面積要素に含めて$d\bm{S}=\bm{n}dS$とし

    \begin{align} \int_S \bm{A}\cdot d\bm{S} \end{align}

    と表すこともできる。


    面積分の例

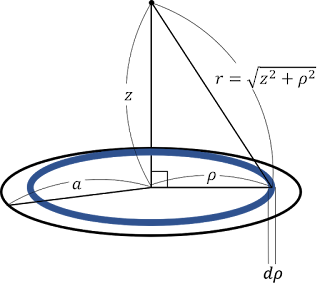
    面積分の例として，次のような問題を考えてみる。

    Q. 半径$a$の円盤上に電荷が面密度（単位面積当たりの密度）$\sigma$で一様に分布しているとき，円盤中心上で面から垂直に$z$離れた位置でのスカラーポテンシャルを求めよ（下図参照）。

    A. 円盤中心からの径座標を$\rho$とすると，(\ref{dS_polar})より，微小面積$ds$上の電荷は$\sigma \rho d\rho d\theta$であるため，その微小面から受けるポテンシャルは

    \begin{align} \frac{\sigma}{4\pi \epsilon_0} \frac{\rho d\rho d\theta}{r} \end{align}

    とおける。 これを$\rho$と$\theta$について積分したものが求める答えだ。

    まずこの中に$\theta$それ自体以外に$\theta$に依存する量はないため，$\theta$積分は容易に実行できて

    \begin{align} \frac{\sigma}{4\pi \epsilon_0} \int_0^a \frac{\rho d\rho }{r} \int_0^{2\pi} d\theta = \frac{\sigma}{4\pi \epsilon_0} \int \frac{2\pi \rho d\rho}{r} \end{align}

    となる。 残るのは$\rho$についての積分だが，三平方の定理より$r=\sqrt{z^2+\rho^2}$であるから積分は

    \begin{align} \frac{\sigma}{4\pi \epsilon_0} \int_0^a \frac{2\pi \rho d\rho}{\sqrt{z^2+\rho^2}} \end{align}

    と変形できる。 ここで

    \begin{align} \frac{d}{d\rho} (z^2+\rho^2)^{1/2}=\frac{1}{2} (z^2+\rho^2)^{-1/2} \frac{d}{d\rho} \rho^2 = \frac{\rho}{\sqrt{z^2+\rho^2}} \end{align}

    を用いると$\rho$積分はスムーズに実行でき

    \begin{align} \phi =\frac{\sigma}{4\pi \epsilon_0} \int_0^a \frac{2\pi \rho d\rho}{\sqrt{z^2+\rho^2}} =\frac{\sigma}{2\epsilon_0}\left( \sqrt{z^2+a^2} - z \right) \end{align}

    と答えが得られる。


    参考文献

    目次

    微分積分の基礎

    多変数関数の微分積分