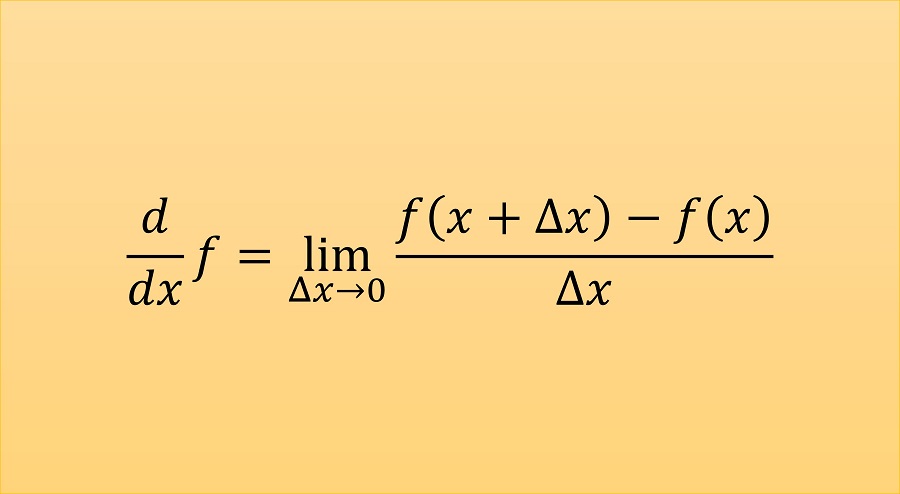はじめに
ここでは，微分の知識を簡潔に提示する。
具体的な関数形（三角関数や指数関数，対数関数など）の微分は，それぞれの解説ページで説明することとして，ここでは基本概念のみを説明することにする。
物理の学習者には，
『微分とNewtonの運動方程式』と合わせて読んでもらえれば，イメージがよりつかみやすくなると思う。
微分と導関数
関数とは
ある値を入れると，別の値を返す規則を関数という。
入力に対応する変数を$x$，返ってくる変数を$y$とすると
\begin{align}
y=f(x)
\end{align}
と表せる。
例えば$y=f(x)=x$という関数であれば，$x=1$のとき$y=1$，$x=2$のとき$y=2$などとなる。
あるいは$y=f(x)=x^2$という関数であれば，$x=1$のとき$y=1^2=1$，$x=2$のとき$y=2^2=4$といった具合である。
$x$の取りうる範囲を実数全体としてそれを横軸に，対応する$y$の値を縦軸にとってこの対応関係をグラフに記していくと，$f(x)=x$および$y=x^2$という関数はそれぞれ以下のように表せる。
関数の変化率
$x$軸（横軸）上の2点$x$と$x + \Delta x $を取り，それらの点に対応する$f(x)$の値の差$\Delta f \equiv f(x+\Delta x)-f(x)$を，$\Delta x$で割ったもの
\begin{align}
\frac{\Delta f}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}
\end{align}
は，グラフ上の2点$(x,f(x))$と$(x+\Delta x,f(x+\Delta x))$をつなぐ直線の傾きを表しており，変数に具体的な値を代入したとき，平均変化率と呼ばれる。
これに対し，$\Delta x$を限りなく小さくした
\begin{align}
\label {def:diff}
\frac{df}{dx} \equiv \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\end{align}
を$f$の導関数といい，導関数を求める操作を微分という。
変数$x$に具体的な値を入れたとき，$df/dx$は瞬間変化率と呼ばれる。
具体的な計算の仕方は次の節以下で見る。
簡単な例
べき関数の微分
具体例として，$f(x)=x^2$の微分を考えてみる。
$x+\Delta x$においてこの関数は
\begin{align}
f(x+\Delta x) = (x+\Delta x)^2 = x^2+ 2x\Delta x +(\Delta x)^2
\end{align}
であるため，微分の定義(\ref{def:diff})に入れると
\begin{equation}
\begin{split}
\frac{df}{dx}
=& \lim_{\Delta x \to 0}\frac{ \{ x^2+ 2x\Delta x +(\Delta x)^2 \}-x^2}{\Delta x} \\
=& \lim_{\Delta x \to 0}\frac{ 2x\Delta x +(\Delta x)^2}{\Delta x} \\
=& \lim_{\Delta x \to 0} (2x +\Delta x )
\end{split}
\end{equation}
となる。
$\lim_{\Delta x \to 0}$というのは，$\Delta x$を限りなく$0$に近づけるということなので，1項目だけが残り
\begin{align}
\frac{df}{dx}=\frac{d}{dx}x^2= 2x
\end{align}
という結果が得られる。
次に，$f(x)=x^3$についても同様に計算してみる。
この場合
\begin{align}
f(x+\Delta x) = (x+\Delta x)^3 = x^3 +3x^2 \Delta x + 3 x (\Delta x)^2+ (\Delta x)^3
\end{align}
なので，$f$の微分は定義より
\begin{equation}
\begin{split}
\frac{df}{dx}
=& \lim_{\Delta x \to 0}\frac{\{ x^3 +3x^2 \Delta x + 3 x (\Delta x)^2+ (\Delta x)^3 \} -x^3}{\Delta x} \\
=& \lim_{\Delta x \to 0}\frac{ 3x^2 \Delta x + 3 x (\Delta x)^2+ (\Delta x)^3}{\Delta x} \\
=& \lim_{\Delta x \to 0} (3x^2 +3x \Delta x + (\Delta x)^2 ) \\
=& 3x^2
\end{split}
\end{equation}
という結果が得られる。
これらの一般化として，任意の自然数$n=0,1,2,3,...$について
\begin{align}
\frac{d}{dx} x^n =nx^{n-1}
\end{align}
が成り立つ。
この公式は$n$を実数に置き換えても成り立つ。
このことは，対数の微分を使って示すことができる。
定数の微分
次に，定数を含んだ関数の微分を考えてみる。
定数とは値が変化しない数のことだ。
よって，例えば$f(x)=x^2+2$のような関数は，$x$がどんな値を取ろうが$+2$の部分に変化はない。
そのため，定義に従って計算すると
\begin{align}
\frac{df}{dx}
=& \lim_{\Delta x \to 0}\frac{ \{ x^2+2x \Delta x+ (\Delta x)^2+ 2 \}-(x^2+2)}
{\Delta x} \notag \\
=& \lim_{\Delta x \to 0}\frac{ \{ x^2+2x \Delta x + (\Delta x)^2 \}-x^2}
{\Delta x} = 2x
\end{align}
となり，定数の寄与は消える。
同様の理由から，定数自体の微分も$0$になる：
\begin{align}
\frac{d}{dx} C=0, \ \ C\text{は定数}
\end{align}
関数$y=f$の値が$x$によらず一定であるということは，以下の図のように傾きの無い直線に対応する。
表記
微分を2回行って得られる関数，2階の導関数は
\begin{align}
\frac{d^2 f}{dx^2} = \frac{d}{dx} \frac{df}{dx}
\end{align}
と表される。
$n$階の微分についても同様に
\begin{align}
\frac{d^n f}{dx^n} = \frac{d}{dx}... \frac{d}{dx} f
\end{align}
である。
微分の略記として，プライム「'」を用い
\begin{align}
f' = \frac{d}{dx} f
\end{align}
が用いられる。
2階の微分なら$f''$，3回なら$f'''$などとも表されるが，高次になると見づらいので，その場合$n$階の導関数は$f^{(n)}$と表される。
物理では，時間$t$に関する微分を
\begin{align}
\dot{f} = \frac{d}{dt} f
\end{align}
と表すことも一般的である。
合成関数の微分
先には，単純な例として$y=x^2$という関数の微分を考えたが，今度は$x$もまた，別の変数$t$の関数として$x=t^2$と表される場合を考えよう。
$y$は$x$の値で決まる関数であるから
\begin{align}
y=f(x)
\end{align}
と表せたのに対し，$x$は$t$の関数であるから
\begin{align}
x =g(t)
\end{align}
と表せる。
このとき
\begin{align}
y=f(g(t))
\end{align}
あるいは
\begin{align}
y=(f \circ g)(t)
\end{align}
という表し方がなされる。
つまり，$t$がまず$g$という関数によって$x$に対応付けられ，その後$f$によって$y$に対応付けられることによって，$t$と$y$の対応付けがなされる。
このような関数を合成関数という。
変数が$t$から$t+\Delta t$に変化したとき，対応する$g$の変化に伴って$f$も変化する。
よって，合成関数$f(g(t))$の$t$に関する微分は
\begin{align}
\frac{d}{dt}f(g(t))
=
\lim_{\Delta t \to 0} \frac{f(g(t+\Delta t))- f(g(t)) }{\Delta t}
\end{align}
と書かれる。
この式は
\begin{align}
1 = \frac{g(t+\Delta t) -g(t) }{g(t+\Delta t)- g(t) }
\end{align}
を差し込むと
\begin{align}
\label {dfg}
\frac{d}{dt}f(g(t))
=
\lim_{\Delta t \to 0} \frac{f(g(t+\Delta t))- f(g(t)) }{g(t+\Delta t) -g(t) }
\cdot \frac{g(t+\Delta t) -g(t) }{\Delta t}
\end{align}
と変形できる。
$\Delta t \to 0$に伴って$\Delta g \equiv g(t+\Delta t) -g(t)$も$0$に近づくため(\ref{dfg})は
\begin{align}
\frac{d}{dt}f(g(t))
=&
\lim_{\Delta t \to 0} \frac{f(g(t+\Delta t))- f(g(t)) }{\Delta g }
\cdot \frac{\Delta g }{\Delta t} \notag \\
=& \frac{df}{dg} \frac{dg}{dt}
\end{align}
と計算できる。
\begin{align}
\frac{dy}{dt} = \frac{dy}{dx}\frac{dx}{dt}
\end{align}
とも表せる。
この計算では，$\Delta t$を$0$に近づける途中で$\Delta g = g(t+\Delta t) -g(t)$が$0$になってしまい，$\Delta f/\Delta g$が発散してしまう可能性を考慮していないため完全なものではないが，ほとんどの場合この導出で十分だ。
最初に挙げた例でいえば
\begin{align}
\frac{dy}{dx}= 2x=2t^2, \ \ \frac{dx}{dt} = 2t
\end{align}
であるから
\begin{align}
\frac{dy}{dt}= 2t^2\times 2t=4t^3
\end{align}
と計算できる。
このように，合成関数の導関数は，それぞれの関数の導関数の積で与えられる。
これを，連鎖律（チェーンルール）と呼ぶ。
関数の積の微分
次に，どちらも$x$の関数である2つの関数$f(x)$と$g(x)$の積$f(x)g(x)$の微分を考える。
これも定義に従えば
\begin{align}
\label {dfxgx}
\frac{d}{dx}(f(x)g(x))
=
\lim_{\Delta x \to 0} \frac{f(x+\Delta x)g(x+\Delta x)- f(x)g(x) }{\Delta x}
\end{align}
である。
今度はここで
\begin{align}
0=-f(x)g(x+\Delta x)+f(x)g(x+\Delta x)
\end{align}
を分子に差し込む。
すると(\ref{dfxgx})は
\begin{align}
\frac{d}{dx}&(f(x)g(x)) \notag \\
=&
\lim_{\Delta x \to 0} \frac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x+\Delta x)+f(x)g(x+\Delta x) -f(x)g(x) }{\Delta x} \notag \\
=&
\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x) }{\Delta x}g(x+\Delta x)
+
\lim_{\Delta x \to 0} f(x)\frac{g(x+\Delta x) -g(x) }{\Delta x}\notag
\end{align}
と変形できる。
$\lim_{\Delta x \to 0}g(x+\Delta x)=g(x)$より1項目は
\begin{align}
\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x) }{\Delta x}g(x+\Delta x)
=
\frac{df(x)}{dx}g(x)
\end{align}
2項目もそのまま
\begin{align}
\lim_{\Delta x \to 0} f(x)\frac{g(x+\Delta x) -g(x) }{\Delta x}
=
f(x)\frac{dg(x)}{dx}
\end{align}
であるから結局
\begin{align}
\frac{d}{dx}(f(x)g(x))=\frac{df(x)}{dx}g(x)+f(x)\frac{dg(x)}{dx}
\end{align}
という一般的な公式が得られる。
