電磁ポテンシャルとゲージ変換

Dr. SSS 2020/05/16 - 11:21:31 1851 電磁気学

はじめに

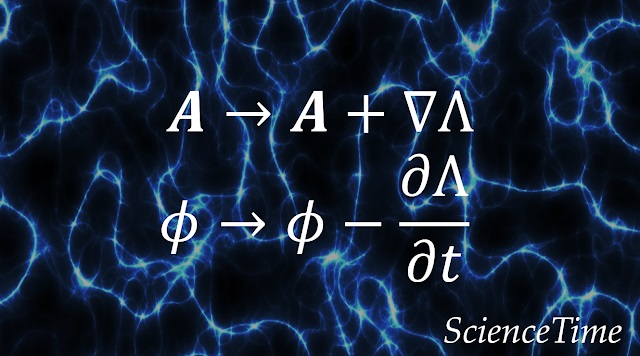
ここでは，電磁ポテンシャルを導入し，ゲージ変換について説明する。そして，ゲージ変換の具体例を用いて，Maxwell方程式の有用な書き換えを行うプロセスについても説明する。

keywords: 電磁気学, Ampèreの法則, ゲージ場, 波動, ゲージ変換, Maxwellの方程式

内容

準備と復習

ベクトル公式

以下の議論では，次の2つのベクトル公式を用いる。 1つ目は，任意のスカラー関数$\phi$が満たす関係

\begin{align} \label{vec1} \nabla \times \nabla \phi=0 \end{align}

である。もう1つは，任意のベクトル$\bm{A}$が満たす

\begin{align} \label {vec2} \nabla \cdot (\nabla \times \bm{A})=0 \end{align}

である。

これらは，成分ごとに計算してみれば直ちに確認できる。本題に入る前にエクササイズとして確認しておいてもいいだろう。直交座標系の成分を$(x_1, x_2, x_3)$と表せば，1つ目の第1成分は

\begin{align} (\nabla \times \nabla \phi)_1 = \pd_2 \pd_3 \phi - \pd_3 \pd_2 \phi = 0 \end{align}

となる。ここで$\pd_i = \pd/\pd x_i \ (i=1,2,3)$である。その他の成分についても添え字を順番に入れ替えて同様の結果を示すことができる。 2つ目の公式は

\begin{equation} \begin{split} \nabla \cdot (\nabla \times \bm{A}) =&\ \pd_1 \left(\pd_2 A_3 -\pd_3 A_2 \right) \\ &+\pd_2 \left(\pd_3 A_1 -\pd_1 A_3 \right) \\ &+\pd_3 \left(\pd_1 A_2 -\pd_2 A_1 \right) \end{split} \end{equation}

となり，2項ずつが対となりキャンセルするため，恒等的に0であることが確かめられる。

Maxwell方程式

Maxwell方程式も改めて列挙しておこう：

電場のGaussの法則
\begin{align} \label {Egauss} \nabla\cdot\bm{E}=\frac{\rho}{\varepsilon_0} \end{align}
磁場のGaussの法則
\begin{align} \label {Bgauss} \nabla \cdot \bm{B}=&0 \\ \end{align}
電磁誘導の法則
\begin{align} \label {rotE} \nabla\times \bm{E} =& -\frac{\pd \bm{B}}{\pd t} \end{align}
Ampère-Maxwellの法則
\begin{align} \label {Amp-Max} \nabla \times \bm{B} =& \mu_0 \left( \bm{j} +\varepsilon_0 \frac{\pd \bm{E}}{\pd t} \right) \end{align}

電磁ポテンシャル

ベクトル公式より，発散がゼロであるベクトル場は，別のベクトル場の回転として表すことができる。よって，この条件

\begin{equation} \nabla \cdot \bm{B}=0 \end{equation}

を満たす磁場$\bm{B}$も，ベクトル場$\bm{A}$を導入して

\begin{equation} \bm{B}=\nabla \times \bm{A} \end{equation}

と表すことができる。この場$\bm{A}$をベクトルポテンシャル（vector potential）と呼ぶ。

ベクトルポテンシャルを電磁誘導の式

\begin{equation} \nabla \times \bm{E} + \frac{\pd \bm{B}}{\pd t}=0 \end{equation}

に代入すると

\begin{equation} \nabla \times \left(\bm{E} + \frac{\pd \bm{A}}{\pd t} \right) =0 \end{equation}

が得られる。カッコ内の量をひとまとめに考え，一つの場とみなすと，それは回転が恒等的にゼロであるベクトル場であることから，スカラー関数の勾配の形における：

\begin{equation} \left(\bm{E} + \frac{\pd \bm{A}}{\pd t} \right) =-\nabla \phi \end{equation}

負号は他の表現との整合性から付加されている。ここで導入される$\phi$を，スカラーポテンシャル（scalar potential）と呼ぶ。 $\phi$と$\bm{A}$を合わせ，電磁ポテンシャル（electromagnetic potentials）と呼ぶ。

改めて，これらのポテンシャルを用いると，電場および磁場はそれぞれ

\begin{align} \bm{B}=&\nabla \times \bm{A} \\ \bm{E}=&-\nabla \phi - \frac{\pd \bm{A}}{\pd t} \end{align}

と表せる。

ゲージ変換

スカラー場の勾配の回転はゼロであるという性質があるため，任意のスカラー関数$\Lambda$を用いてベクトルポテンシャルを

\begin{equation} \bm{A} \to \bm{A} +\nabla \Lambda \end{equation}

と変換しても

\begin{equation} \nabla \times (\bm{A} +\nabla \Lambda) = \nabla \times \bm{A} \end{equation}

となり，磁場は変化しないことがわかる。そして，スカラーポテンシャルも同時に

\begin{equation} \phi \to \phi - \frac{\pd \Lambda}{\pd t} \end{equation}

と変換すれば，電場も不変に保たれる。これらの変換をゲージ変換（gauge transformation）と呼び，これらの変換で不変に保たれる場の性質を，ゲージ不変性（gauge invariance ）という。このゲージ不変性を利用し，問題に応じて適切なゲージ変換を行うことで，電磁場の表現を簡約化することができる。

電場のGaussの法則を電磁ポテンシャルを用いて表現すると

\begin{equation} \label{eq:Gauss_law2} \nabla^2 \phi + \frac{\pd }{\pd t}(\nabla\cdot\bm{A}) =-\frac{\rho}{\varepsilon_0} \end{equation}

となる。同様にAmpèreの法則は

\begin{equation} \label{eq:Amp_law2} \nabla^2 \bm{A} -\frac{1}{c^2} \frac{\pd \bm{A}}{\pd t^2} - \nabla \left ( \nabla \cdot \bm{A} + \frac{1}{c^2} \frac{\pd \phi}{\pd t} \right) =-\mu_0 \bm{j} \end{equation}

となる。

ここで，ゲージ変換の任意性を利用し

\begin{equation} \label{eq:Lorentz_cond} \nabla \cdot \bm{A} + \frac{1}{c^2} \frac{\pd \phi}{\pd t} =0 \end{equation}

を満たすような条件を採用すれば，(\ref{eq:Gauss_law2})と(\ref{eq:Amp_law2})においてスカラーポテンシャルとベクトルポテンシャルは分離され，それぞれ

\begin{align} \label{eq:wave1} \left( \nabla^2 - \frac{1}{c^2} \frac{\pd^2}{\pd t^2} \right) \phi =& -\frac{\rho}{\varepsilon_0} \\ \label{eq:wave2} \left( \nabla^2 - \frac{1}{c^2} \frac{\pd^2}{\pd t^2} \right) \bm{A} =& -\mu_0 \bm{j} \end{align}

に帰着する。これらは，非同次な波動方程式の形をしている。 (\ref{eq:Lorentz_cond})の条件を，Lorentz条件（Lorentz condition）と呼ぶ。

他に有用な条件の一例として

\begin{equation} \nabla \cdot \bm{A}=0 \end{equation}

がある。これは，Coulomb，放射（radiation）, あるいは横波（transverse）ゲージ条件などと呼ばれる。この条件の下では，$\phi$は(\ref{eq:Gauss_law2})より，Poissonの方程式（Poisson's equation）

\begin{equation} \nabla^2 \phi =-\frac{\rho}{\varepsilon_0} \end{equation}

を満たし，$\bm{A}$は

\begin{equation} \left( \nabla^2 - \frac{1}{c^2} \frac{\pd^2}{\pd t^2} \right) \bm{A} = -\mu_0 \bm{j} + \nabla \frac{1}{c}\frac{\pd\phi}{\pd t} \end{equation}

を満たす。