Introduction
ここでは，物理を学ぶ上では必須となる，偏微分について，図を用いてわかりやすく解説する。
決して難しい概念ではないため，構えずにリラックスして読んでもらいたい。
微分の復習
『微分の基礎』で説明したように，変数$x$が増加したときの関数$f(x)$の増分は
\begin{align}
df = \frac{d f}{dx}dx
\end{align}
と書かれた。ここで
\begin{align}
\frac{d }{d x}f(x)=&\lim_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}
\end{align}
である。
偏微分
では，$x$と$y$という2変数の関数$f(x,y)$の場合はどうか。このような関数の変化は
\begin{align}
\label {df}
df =\frac{\pd f}{\pd x} dx + \frac{\pd f}{\pd y} dy
\end{align}
と書かれる。このように，1次までの近似（$dx$や$dy$の2乗の大きさ以降を無視する近似）で変化分を表したのを，全微分という。ここで$dx$の係数は
\begin{align}
\frac{\pd }{\pd x}f(x,y)\equiv&\lim_{\Delta x\to 0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}
\end{align}
で定義され，関数$f$の$x$に関する偏導関数と呼ばれる。
また，偏導関数を求める操作を偏微分という。
このとき，変数$y$は固定した定数として扱われる。$dy$の係数も同様に
\begin{align}
\frac{\pd }{\pd y}f(x,y)\equiv&\lim_{\Delta y\to 0} \frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}
\end{align}
で，$x$を固定した$f$の導関数であり，$y$に関する偏導関数と呼ばれる。
(\ref{df})のイメージは，以下の図1を参照。
図1：全微分のイメージ。$(\pd f(x,y)/ \pd y)$と$(\pd f(x+\Delta x,y)/ \pd y)$の置き換えについては，文末を参照。
具体的な関数において，一方の変数を固定するということをイメージするには，図2を見てもらいたい。
図では$f(x,y)=-x^2-y^2$という関数について，$y=y_0$を固定したときの，$x$方向の$f$の傾きを表している。この例から，$x$を固定した場合や，別の形の関数の場合もイメージしやすくなるだろう。
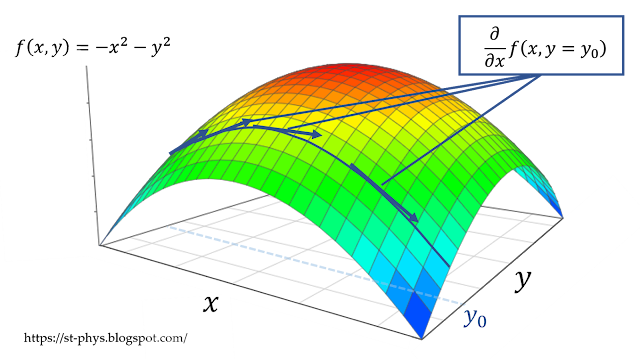図2：他の変数を固定して微分するということのイメージ
偏微分のこれらの議論は，変数が2つの場合だけではなく，任意の個数の場合にも一般化される。独立変数が$(x_1,...x_n)$と$n$個ある場合，(\ref{df})に対応する式は
\begin{align}
df =\frac{\pd f}{\pd x_1} dx_1 + \frac{\pd f}{\pd x_2} dx_2+...+\frac{\pd f}{\pd x_n} dx_n
=\sum_{i=1}^n \frac{\pd f}{\pd x_i} dx_i
\end{align}
となる。
表記
偏微分の表記として，
\begin{align}
\left( \frac{\pd f(x,y)}{\pd x} \right)_y
\end{align}
のように，固定する変数を明示されることもある。特に，独立変数の取り方が自明でない場合などには，このような表記がなされることが多い。
また，省略形として
\begin{align}
f_x=&\frac{\pd f}{\pd x} , \notag \\
f_{xx}=& \frac{\pd^2 f}{\pd x^2}, \\
f_{xy}=&\frac{\pd^2 f}{\pd x \pd y} \notag
\end{align}
などが用いられることもある。二つ目以降は二階の偏微分であり，最後の例は$x$および$y$でそれぞれ他の変数を固定しながら微分するという意味である。
例題
最後に，いくつか例題を示そう。
Q. $f(x,y)=-x^2-y^2$を$x$で偏微分してみよう。
A.
\begin{align}
\notag
\frac{\pd}{\pd x}f(x,y)=&
-\frac{\pd}{\pd x}(x^2)-{\frac{\pd}{\pd x}(y^2)} \\
\notag
=&-2x
\end{align}
Q. $f(x,y)=x^2y$を$x$および$y$で順に偏微分してみよう。
A.
\begin{equation}
\notag
\begin{split}
\frac{\pd}{\pd x}(x^2y)=&2xy \\
\frac{\pd^2}{\pd x \pd y}(x^2y)=&\frac{\pd}{\pd y}(2xy) \\
=& 2x
\end{split}
\end{equation}
Q. 最後に，図1にある
\begin{align}\label {repl}
\frac{\pd f(x,y)}{\pd y} \simeq \frac{\pd f(x+\Delta x,y)}{\pd y}
\end{align}
の正当性を示そう。
A. これらの二つの関数の差を取ると
\begin{align}
\notag
\frac{\pd f (x+\Delta x,y)}{\pd y}-\frac{\pd f(x,y)}{\pd y}
=\frac{\pd^2 f(x,y)}{\pd x \pd y} \Delta x
\end{align}
となり，$\Delta x\to 0$の極限で
\begin{align}
\notag
\frac{\pd f(x+\Delta x,y)}{\pd y} dy =
\frac{\pd f (x,y)}{\pd y} dy
+\frac{\pd^2 f(x,y)}{\pd x \pd y} dy dx
\end{align}
と微小量の2次の違いしかなくなるため，1次近似(\ref{df})に入れたとき，(\ref{repl})の間で置き換えが可能になる。
