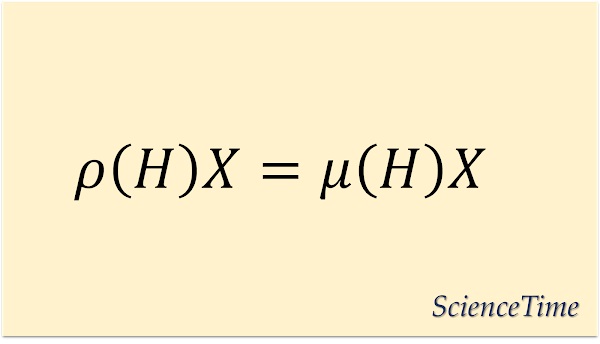はじめに
半単純Lie代数の任意の表現は,既約表現の直和として得られる。 対して,半単純Lie代数の既約表現はLie代数の表現行列の固有値として与えられるウェイトの中で最大のもの,最高ウェイトにより一意に定められる。 ここでは,そのLie代数の表現のウェイトについて解説する。
ウェイトの定義
$\frg$を複素半単純Lie代数,$\frh$をその固定されたCartan部分代数とし,$H_1,...,H_l$をその基底とする。 $\frg$の元は互いに可換であるから,$\frg$の表現$(\rho,V)$に対し
\begin{align} \rho(H_i)X=m_iX \end{align}
を満たす固有ベクトル$X\in V$が存在し,表現行列$ \rho(H_i)$は同時対角化可能である。
任意の$H\in \frh$は$H=\sum_{i=1}^l a^i H_i$と展開でき,それに対して$H_1,...,H_l$ の双対基底$\bm{e}^1,...,\bm{e}^l$を用いて
\begin{align} \mu=\sum_{i=1}^l m_i\bm{e}^i \end{align}
とできるから,任意の$H\in \frh$に対して
\begin{align} \label{eq:weight} \rho(H)X=\mu(H)X \end{align}
が成り立つ。 固有値$\mu(H)$を与える$\mu$を表現$\rho$のウェイト(weight)という。
定義からわかるよう,ルートとは随伴表現という特定の表現のウェイトのことである。
固有ベクトル
$H\in \frh$の何らかの表現行列$\rho(H)$のウェイト$\mu$に対応する固有ベクトルを$|\mu \rangle$と表す:
\begin{align} \rho(H)|\mu \rangle = \mu |\mu \rangle \end{align}
物理的な応用をイメージして,この固有ベクトルを「状態」と呼ぶことにしよう。
\begin{align} \rho([H,E_{\pm\alpha}]) = [\rho(H)\rho(E_{\pm\alpha})] = \pm\alpha\rho(E_{\pm\alpha}) \end{align}
であるから,$\rho(E_{\pm\alpha})$を作用した状態を考え,それに対して$\rho(H)$を作用してみると
\begin{align} \rho(H)\rho(E_{\pm\alpha})|\mu \rangle &= \left([\rho(H)\rho(E_{\pm\alpha})]+\rho(E_{\pm\alpha})\rho(H)\right) |\mu \rangle \notag \\ &= (\mu\pm\alpha)\rho(E_{\pm\alpha}) |\mu \rangle \end{align}
となり,状態$\rho(E_{\pm\alpha}) |\mu \rangle$は固有値$(\mu\pm\alpha)$に対応する固有ベクトルとなっていることがわかる。 よって,係数$N_{\pm\alpha,\mu}$を用いて
\begin{align} \label{eq:weight_N} \rho(E_{\pm\alpha}) |\mu \rangle = N_{\pm\alpha,\mu}|\mu \pm \alpha\rangle \end{align}
と表すことができる。
ウェイトは有限であるから,この操作を繰り返すことで,ウェイトの系列
\begin{align} \label{eq:weight_series} \mu-q\alpha,\mu-(q-1)\alpha,...,\mu,...,\mu+(p-1)\alpha,\mu+p\alpha \end{align}
が得られる($q,p$は0以上の整数)。
$N_{\alpha,\mu}$の決定
以下,$\rho(H)$,$\rho(E_\alpha)$などを省略し,単に$H$や$E_\alpha$のように表す。
$N_{\alpha,\mu}$は次のようにして決められる。 (\ref{eq:weight_series})の形のウェイトの系列を考える。 異なるウェイト$\mu,\nu$に対し
\begin{align} \langle \mu | \nu \rangle = \delta_{\mu,\nu} \end{align}
と規格化する。
すると
\begin{equation} \begin{split} (\alpha,\mu) =& g^{ij}a_im_j \\ =& \langle \mu | a^i H_i | \mu \rangle \\ =& \langle \mu | [E_\alpha,E_{-\alpha}] | \mu \rangle \\ =& \langle \mu | E_\alpha E_{-\alpha} | \mu \rangle -\langle \mu |E_{-\alpha} E_\alpha | \mu \rangle \\ =& \langle \mu | E^\dagger_{-\alpha} E_{-\alpha} | \mu \rangle -\langle \mu |E^\dagger_\alpha E_\alpha | \mu \rangle \\ =& |N_{-\alpha,\mu}|^2 -|N_{\alpha,\mu}|^2 \end{split} \end{equation}
となる。 また
\begin{equation} \begin{split} N_{-\alpha,\mu} =& \langle \mu-\alpha|E_{-\alpha}|\mu\rangle \\ =& \langle \mu-\alpha|E^\dagger_{\alpha}|\mu\rangle \\ =& \langle \mu|E_{\alpha}|\mu-\alpha\rangle^* = N^*_{\alpha,\mu-\alpha} \end{split} \end{equation}
が成り立つから
\begin{align} \label{eq:N_series} |N_{\alpha,\mu-\alpha}|^2 -|N_{\alpha,\mu}|^2 = (\alpha,\mu) \end{align}
という漸化式を得る。
ウェイトが有限であることより
\begin{align} E_\alpha|\mu+p\alpha\rangle =0, \quad E_{-\alpha}|\mu-q\alpha\rangle =0 \end{align}
すなわち
\begin{align} N_{\alpha,\mu+p\alpha}=0 \\ N_{-\alpha,\mu-q\alpha} = N_{\alpha,\mu-(q+1)\alpha}=0 \end{align}
が成り立つから,(\ref{eq:N_series})を順に並べると
\begin{align}
|N_{\alpha,\mu+(p-1)\alpha}|^2 - \underbrace{|N_{\alpha,\mu+p\alpha}|^2}_{=0} =& (\alpha,\mu)+p(\alpha,\alpha) \notag \\
|N_{\alpha,\mu+(p-2)\alpha}|^2 - |N_{\alpha,\mu+(p-1)\alpha}|^2 =& (\alpha,\mu)+(p-1)(\alpha,\alpha) \notag \\ %%% \vdots \notag \\
%%%
\label{eq:N2_series}
|N_{\alpha,\mu}|^2 - |N_{\alpha,\mu+\alpha}|^2 =& (\alpha,\mu)+(\alpha,\alpha) \\ |N_{\alpha,\mu-\alpha}|^2 -
|N_{\alpha,\mu}|^2 =& (\alpha,\mu) \notag \\
%%%
\vdots \notag \\
%%%
|N_{\alpha,\mu-q\alpha}|^2 - |N_{\alpha,\mu-(q-1)\alpha}|^2 =& (\alpha,\mu)-(q-1)(\alpha,\alpha) \notag \\
\underbrace{|N_{\alpha,\mu-(q+1)\alpha}|^2}_{=0} - |N_{\alpha,\mu-q\alpha}|^2 =& (\alpha,\mu)-q(\alpha,\alpha) \notag \end{align}
となる。 これをすべて足し合わせると,左辺はキャンセルし,右辺は$(\alpha,\alpha)$を等差とする数列であるから
\begin{align} 0 = (p+q+1)\left( (\alpha,\mu)-\frac{q-p}{2}(\alpha,\alpha) \right) \end{align}
という関係が得られ,これよりウェイト一般に関する,ルートと同様の関係
\begin{align} \label{eq:w_integer} q-p=\frac{2(\alpha,\mu)}{(\alpha,\alpha)} \end{align}
が導かれる。
また,(\ref{eq:N2_series})の真ん中から上に向かって
\begin{equation} \begin{split} |N_{\alpha,\mu}|^2 =& (\alpha,\mu+\alpha) + |N_{\alpha,\mu+\alpha}|^2 \\ =& (\alpha,\mu+\alpha) + (\alpha,\mu+2\alpha) + |N_{\alpha,\mu+2\alpha}|^2 \\ \vdots \end{split} \end{equation}
と代入操作を繰り返していくことで
\begin{align} |N_{\alpha,\mu}|^2 = \sum_{k=1}^p (\alpha,\mu+k\alpha) = p\left( (\alpha,\mu)-\frac{p+1}{2}(\alpha,\alpha) \right) \end{align}
となり,(\ref{eq:w_integer})を用いてさらに変形することで
\begin{align} |N_{\alpha,\mu}|^2 = p(q+1) \frac{(\alpha,\alpha)}{2} \end{align}
が得られる。