群論 2021-07-04

ルート空間分解とCartan-Weyl基底

ScienceTime Team
112 views
ルート空間分解とCartan-Weyl基底
Keywords:
Lie群 Lie代数 固有値問題 線形代数 固有空間 群の表現 随伴表現 Killing形式

Introduction

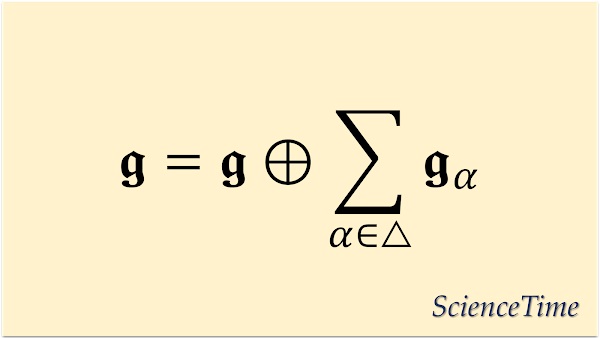
ここでは，Cartan部分代数とルートの性質を利用してLie代数を直和分解し，Lie代数の構造を調べるにあたって有用となる新たな基底を導入する。

ルート空間とルート空間分解

まず，『Cartan部分代数とルート』の内容を，数学的により形式的な形で記述しなすことでおさらいしよう。

Lie代数$\frg$のCartan部分代数$\frh$を固定したとき，任意の元$H\in \frh$に対し，同時固有ベクトル$X\in \frg$が存在し

\begin{align} \label{eq:eigen_adX} \ad(H)X=\alpha(H)X \end{align}

が成り立つ（コチラも参照）。 このとき，$\frh$の双対空間$\frh^*$の元$\alpha$を，$\frg$のルートという。

ここで，新たな記号を導入し，0でないルートの集合を$\bigtriangleup$と記すこととする。 これは，$(\dim \frg- \dim \frh)$個の元からなる有限集合である。

$\ad(H)$は対角化可能であるから，各$\alpha \in \frh^*$に対し $\frg$の固有空間

\begin{align} \mathfrak{g}_\alpha = \{ X\in \mathfrak{g} \ | \ \ad(H)X=\alpha(H)X, \ \forall H\in \mathfrak{h} \} \end{align}

が定まり，$\frg$を

\begin{align} \label{eq:root_decomp} \frg=\frg_0\oplus \sum_{\alpha \in \bigtriangleup} \frg_\alpha \end{align}

と直和分解することができる。 このとき，$\frg_\alpha$をルート$\alpha$に対応するルート空間（root space）といい，(\ref{eq:root_decomp})を$\frg$のルート空間分解（root space decomposition）という。

$\frg_0$は

\begin{align} \ad(H)X=[H,X]=0 \end{align}

となる$X$すべての集合であるが，$\frh$自身がこうした集合で極大なもののことであるから，$\frg_0=\frh$である。


Cartan-Weyl基底

$E_\alpha \in \frg_\alpha$であったから，$\{H_\alpha, E_\alpha, E_{-\alpha}\}$によって，新たに$\frg$の基底を構成することができる。 また，$[E_\alpha,E_\beta]$は固有値$\alpha+\beta$に対応する固有値であったから，$\alpha+\beta$もルートであるなら，何らかの数$N_{\alpha,\beta}$を用いて

\begin{align} [E_\alpha,E_\beta]=N_{\alpha,\beta}E_{\alpha+\beta}\in \frg_{\alpha+\beta} \end{align}

と表すことができる。 このとき

\begin{align} & N_{\alpha,\beta} = -N_{-\alpha,-\beta}, \notag \\ \label{eq:Nab-N-a-b} & B(E_\alpha,E_{-\alpha})= 1 \end{align}

が同時に成り立つよう$E_\alpha$を選ぶことができる。

これまでの結果をまとめると，このようにして選んだ基底は次のような交換関係を満たす：

\begin{equation} \begin{split} &[H_i, H_j] = [H_\alpha,H_\beta]=0 \\ % &[H_i, E_{\pm \alpha}] = \pm a_i E_{\pm\alpha} \\ % &[E_\alpha,E_\beta] = \left\{ \begin{array}{cc} H_\alpha =\sum_{i=1}^l a^i H_i & \text{if} \ \alpha+\beta=0 \\ N_{\alpha,\beta}E_{\alpha+\beta} & \text{if} \ \alpha+\beta \in \bigtriangleup \\ 0 & \text{if} \ \alpha+\beta \notin \bigtriangleup \end{array} \right. \end{split} \end{equation}

（$l=\dim \frh$）

(\ref{eq:Nab-N-a-b})と合わせ，これらの関係を満たす基底を，Cartan-Weyl基底または標準基底（canonical basis）という。


References

  • Arvanitogeōrgos, A. (2003). An Introduction to Lie groups and the Geometry of Homogeneous Spaces. American Mathematical Society.
  • Bincer, A. M. (2013). Lie Groups and Lie Algebras: A Physicist's Perspective. Oxford University Press.
  • Das, A., & Okubo, S. (2014). Lie Groups and Lie Algebras for Physicists. World Scientific.
  • Georgi, H. (2018). Lie Algebras in Particle Physics: From Isospin to Unified Theories. CRC Press.
  • 佐藤 肇. (2000). リー代数入門: 線形代数の続編として. 裳華房.
  • 島和久. (1981). 連続群とその表現. 岩波書店.