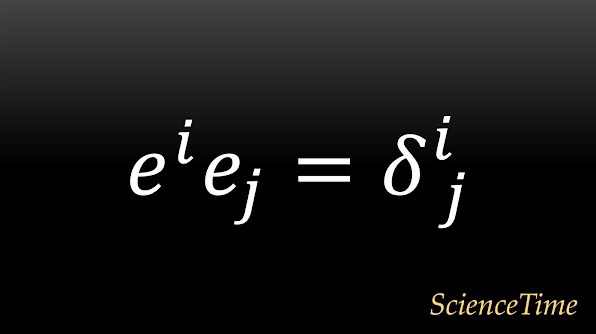双対空間と反変ベクトル・共変ベクトル

はじめに

ここでは，ベクトル空間の双対空間と，反変ベクトル，共変ベクトルという概念について説明する。

keywords: ベクトル解析, 線形代数, ベクトル空間, 線形変換

内容

双対空間

ベクトル空間$V$から$R$への線形写像$\omega$を考える。この写像が線形であるとは，すなわち，任意の$a,b\in R$と$\bm{x},\bm{y}\in V$について

\begin{align} \label{eq:def_lin} \omega(a\bm{x}+b\bm{y})=a\omega(\bm{x})+b\omega(\bm{y}) \end{align}

が成り立つということである。そしてまた，この写像について和とスカラー倍がそれぞれ

$(\omega_1+\omega_2)(\bm{x})=\omega_1(\bm{x})+\omega_2(\bm{x})$
$(a\omega)(\bm{x})=a(\omega(\bm{x}))$

と定義できる。これらが線形性の定義(\ref{eq:def_lin})を満たすことは直ちに確かめられる。

すると，この関数もまたベクトル空間を構成する。これを，ベクトル空間$V$の双対空間（dual space）といい，$V^*$と表す。そして，$V^*$の元を，コベクトル（covector）や1形式（1-form）などと呼ぶ。

双対基底

$n$次元ベクトル空間$V$の任意のベクトル$\bm{x}$は，基底$\{\bm{e}_i\}$を用いて

\begin{align} \label{eq:x_xe} \bm{x}=\sum_{i=1}^n x^1 \bm{e}_1+...+x^n\bm{e}_n \end{align}

と展開できる。成分の添え字を上付きにしていることは気まぐれではなく重要なものなので注意してほしい。また，毎回和の記号を書くのは煩わしいので，上下同じ添え字を持つ量が同じ項にある場合は，和の記号がなくとも和を取ることとする。すなわち

\begin{align} a^i b_i=a^1b_1+a^2 b_2+... \end{align}

である（Einsteinの規約）。

$V$のベクトルの展開(\ref{eq:x_xe})に対し，$V$の双対空間$V^*$の元として，$\bm{x}$をその$i$番目の成分に対応付ける写像

\begin{align} \label{eq:omegai} u^i(\bm{x})=x^i \end{align}

を考えることができる。特に，$\bm{x}=\bm{e}_j$と取れば，この写像は

\begin{align} u^i(\bm{e}_j)=\delta^i_{\ j} \end{align}

となる。

また，任意の$\omega \in V^*$に対し

\begin{align} \omega_i \equiv \omega(\bm{e}_i) \end{align}

とする。すると，任意の$\bm{x}=x^j \bm{e}_j \in V$に対して

\begin{align} \omega(\bm{x}) = \omega \left(x^j \bm{e}_j \right) = x^j \omega(\bm{e}_j) = \omega_j u^j(\bm{x}) \end{align}

となるから，すなわち

\begin{align} \omega=\omega_j u^j \end{align}

が成り立つことがわかる。これは

\begin{align} \bm{e}^i\equiv u^i \end{align}

と表すとよりわかりやすいが，任意の$\omega \in V^*$は，互いに線形独立な$\{\bm{e}^1,...,\bm{e}^n\}$の組を基底として

\begin{align} \omega = \omega_i \bm{e}^i \end{align}

と展開できることを示している。よって，これら$\{\bm{e}^1,...,\bm{e}^n\}$を，$V$の基底$\{\bm{e}_1,..,\bm{e}_n\}$の双対基底（dual basis）と呼ぶ。

反変ベクトルと共変ベクトル

基底の取り換えに伴い，$\bm{x} =x^i \bm{e}_i \in V$の成分および基底は，線形変換$P^i_{\ j}$を用いてそれぞれ

\begin{align} {x'}^j =& (P^{-1})^j_{\ i} x^i \\ \label{eq:e_trns} \bm{e}'_j =& P^i_{\ j}\bm{e}_i \end{align}

と変換されるのであった。では，双対空間のベクトルの成分と基底はそれぞれどのように変換されるだろうか。

ベクトル空間の基底とその双対基底の間には

\begin{align} \label{eq:ee_delt} \bm{e}^i (\bm{e}_j)=\delta^i_{\ j} \end{align}

という関係が成り立つのであった。これに$P^j_{\ k}$を作用させると

\begin{align} \bm{e}^i (\bm{e}'_k)=P^i_{\ k} \end{align}

であり，続けて線形変換の逆行列$P^{-1}$を作用させることで

\begin{align} (P^{-1})^j_{\ i}\bm{e}^i (\bm{e}'_k) = \delta^j_{\ k} \end{align}

となる。これを(\ref{eq:ee_delt})と比較すると，双対基底が

\begin{align} {\bm{e}'}^j = (P^{-1})^j_{\ i}\bm{e}^i \end{align}

と変換されることがわかる。これは，$V$上のベクトルの成分と同様の変換規則である。

これよりまた，$V^*$上のベクトルの成分が，$V$上のベクトルの基底と同様の変換則(\ref{eq:e_trns})に従い

\begin{align} \omega'_j = P^i_{\ j} \omega_i \end{align}

と変換されることもわかる。このことから，$V^*$のベクトルは共変ベクトル（covariant vector）と呼ばれる。対して，$V$のベクトルは成分がその基底とある種反対に変換されるため，反変ベクトル（contravariant vector）と呼ばれる。

双対空間と反変ベクトル・共変ベクトル

双対空間

双対基底

反変ベクトルと共変ベクトル

参考文献